Uncontrolled manifold analysis (UCM) is a technique for analysing a high-dimensional movement data set with respect to the outcome or outcomes that count as successful behaviour in a task. It measures the variability in the data with respect to the outcome and decomposes it into variability that, if unchecked, would lead to an error and variability that still allows a successful movement.
In the analysis, variability that doesn’t stop successful behaviour lives on a manifold. This is the subspace of the values of the performance variable(s) that lead to success. When variability in one movement variables (e.g. a joint angle, or a force output) is offset by a compensation in one or more other variables that keeps you in that subspace, these variables are in a synergy and this means the variability does not have to be actively controlled. This subspace therefore becomes the uncontrolled manifold. Variability that takes you off the manifold takes you into a region of the parameter space that leads to failure, so it needs to be fixed. This is noise that needs control.
With practice, both kinds of variability tend to decrease. You produce particular versions of the movement more reliably (decreasing manifold variance, or V-UCM) and you get better at staying on the manifold (decreasing variance living in the subspace orthogonal to the UCM, or V-ORT). V-UCM decreases less, however (motor abundance) so the ratio between the two changes. Practice therefore makes you better at the movement, and better at allocating your control of the movement to the problematic variability. This helps address the degrees of freedom control problem.
My current interest is figuring out the details of this and related analyses in order to apply it to throwing. For this post, I will therefore review a paper using UCM on throwing and pull out the things I want to be able to do. All and any advice welcome!
Yang & Scholz (2005) analysed learning in a throwing task using UCM. The task was learning to throw a Frisbee onto a horizontal target 6.15m away. The participants threw from a seated position, strapped into a chair; this restricted the movement to the throwing arm. 6 participants threw 750 training throws, and 3 of them came back to do 1800-2700 more trials.
The data was composed 10 joint angle time series per throw. The variability in these time series was partitioned into V-UCM and V-ORT defined with respect to several performance variables hypothesised to be candidate controlled outcomes; movement extent, movement direction, hand path velocity, and hand’s orientation with respect to the target (there were some other analyses, but they are not relevant here).
UCM Analysis steps
As far as I can tell (help welcome!) this Jacobian matrix is a mapping function that implements the change you get in a performance variable when the joint configuration changes. In other words, the matrix is some kind of differential function. Once you have this mapping function, you can find the null space, the region in which changes in the joint configuration produce no change in the PV; the differential is 0. Remember you can get this in a multi-dimensional space when changes in one joint angle are compensated for by changes in another joint angle, such that the overall joint configuration remains unchanged with respect to the target value of the PV. In this context, these spaces are the uncontrolled manifold.The first step in the analyses is to determine the geometric model relating each PV [Performance Variable] to the configuration of joint angles. The Jacobian matrix, as an analytic expression of changes in the value of a particular PV as the result of an independent change of a particular joint angle, was then determined, and its null space computed based on the mean joint configuration across relevant trials. The null space is a set of basis vectors that span the space of joint angles and it provides a linear estimate of joint combinations that are consistent with a particular value of the PV of interest. A different null space exists for every value of a given PV and these differ for different PVs. Such null spaces have been referred to as uncontrolled manifolds…pg 142
Once you have this, you take your time series of joint angles for each trial and project it onto a) the null space and b) another subspace orthogonal to that null space. Variability in (a) is V-UCM; variability in the other is V-ORT.
UCM over time
Yang & Scholz did something that I want to do but have heard is problematic; any advice on this welcome! They performed the UCM analysis over time; specifically, they repeated the UCM for each 1% of the normalised trial length (this gives them enough data to compute a meaningful variance while getting a fairly fine temporal resolution on the analysis). They also then looked at the first, middle and final 30% of the data.
What this does, in principle, is tell you whether or not the movement is being organised with respect to your manifold over time; in theory, this can ebb and flow. They then state
The mean value of joint configuration at each point in the movement was considered to correspond to the ‘‘desired’’ value of the PVs for this analysis. This is because it is typically not possible to know what specific value of any PV the CNS is trying to stabilize, particularly during the movement. To the extent that this approximation is wrong, variance in joint space will tend to fall in the space orthogonal to the UCM (higher V-ORT), since the estimate of the UCM is based on the mean value.Here’s what I think this means. At any given moment in time, it’s not a sure thing what the nervous system is trying to do; control with respect to the manifold may not be active throughout the movement, or it may evolve over time. It’s therefore not clear how to interpret a given joint configuration relative to the target PV throughout the movement. They use the mean to account for this, and note that this assumption, if wrong, punishes them by showing up in V-ORT. This justifies the method because it is conservative, i.e. it will make it harder to find evidence of control happening with respect to the UCM.
Some thoughts
- If the movement is not being controlled with respect to the manifold at time t but then is at time t+1, you should see increasing V-UCM around time t as the movement begins to drift and then a decrease in V-UCM at time t+1 as control is re-exerted. Tracking this pattern over time and with respect to multiple candidate controlling performance variables, you should (I think) be able to identify periods of movement under the control of various performance variables and periods of ballistic (feedforward, error accumulating, uncontrolled) movement. This could then index the onset and offset of perceptual control - more on this later!
- Is this analysis problematic? If so, how and why?
Different performance variables, same variability = different manifolds
One cool thing I found out about here is that you can, of course, partition the variability in your joint angle data with respect to more than one manifold. This means you can pit performance variables against one another, and also against themselves (combining being able to do this over time). You can do this by remembering you expect certain patterns across the variability measures depending on whether the system is working as a synergy with respect to a given PV, and other patterns when it’s not. Specifically (refer to Figure 1 in my last post)
- If the candidate PV is not relevant to performance, V-ORT and V-UCM will be roughly equal (there is no synergy working to preserve a small set of values of this PV)
- If the PV is relevant to performance (i.e. shaping the control, defining the synergy) then you should see V(UCM) > V(ORT); variability that takes you off this manifold will get corrected/compensated out.
- The size of the ratio of these is information about how important the PV is, in terms of the strength of the synergy it is defining
Some thoughts
- It occurs to me that this gets complicated if you can also UCM over time. At what point do you do this analysis? Multiple points?
- Obviously, for successful trials, V-ORT will by definition be fairly low; even if the PV isn't the thing being controlled per se, there might still be values it has to take for success to occur. Comparing variability measures across PVs helps here (i.e. you should see the most structure in variability partitioned with respect to the right control PV).
Learning
One of the most useful applications of UCM comes when you wish to evaluate learning; you can track initial variability and watch to see if it becomes more structured over time.
Some thoughts:
- If learning is working to get you on a manifold defined with respect to a performance variable, V-ORT from this manifold will go down over time.
- If learning is also working to stabilise a specific action (i.e. a particularly efficient technique) then V-UCM will also go down. But in general, V-ORT will decrease much faster than any change in V-UCM and V-UCM will remain higher that V-ORT.
- If the analysis is only on successful trials, the relative amount of variability may not change much (V-ORT will be, by definition, pretty low on these trials). This makes me wonder about analysing error trials and whether it’s useful.
Results
This paper has many analyses in it; the relevant one for this post is illustrated in Figure 1.
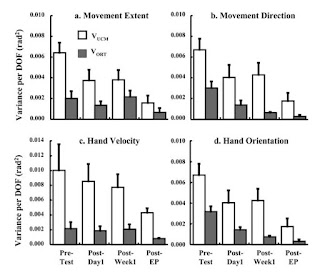 |
| Figure 1. V-UCM (white bars) and V-ORT (grey bars) over training for manifolds defined with respect to 4 different performance variables |
Things to note:
- Overall variability decreased (both components came down) but V-UCM is always higher than V-ORT
- Both showed decreases over time (although lack of power meant the stats don't work out usefully very often).
- Hand velocity showed no real change in V-ORT while the others did; this suggests hand velocity is not being controlled per se. V-ORT came down significantly by the end for the other three PVs.
So what have we learned? UCM analysis makes useful predictions, helps interpret high-dimensional data sets, provides a way to probe the control strategies in play for a movement, and is capable of showing a manifold isn't working (even though set values of hand velocity are required for accurate performance, the variability relative to the production of hand velocity did no show evidence of a manifold). It lets you look over time (maybe) and between performance variables (definitely) and provides a way to look at learning in the motor abundance framework. So far, so very good!
References




No comments:
Post a Comment